A Theory of Progress: Standing On The Shoulders Of Giants

A combinatorial model of progress, explaining historical exponential growth and the occasional periods of stagnation

Related to Isolated Narratives of Progress, Punctuated Equilibria Theory of Progress, The Next S Curve. There’s a more wonky section upfront with the model, then a lit review on how innovation requires recombination of “surprising” elements, and a view on its implications.

---

When people thought the earth was flat, they were wrong. When people thought the earth was spherical, they were wrong. But if you think that that thinking the earth is spherical is just as wrong as thinking the earth is flat, then your view is wronger than both of them put together.

Isaac Asimov

If we cast our eyes back into history, we can see epistemology developing from the time of Epicurus, geometry flowing from axioms from Euclid, systematic observations from Ptolemy and Ibn Haytham, and treatises on how to conduct observations to form hypotheses and then experiments to test them from Bacon in the 1600s. We truly stand on the shoulders of giants.

Introduction

When Newton said that we are "standing on the shoulders of giants", he was being poetic. But he was also being descriptive about the way ideas evolve and science works. And yet, a few centuries later, we're still debating the paths that lead to progress and successive rounds of innovation. It's extraordinarily important as part of the analysis of why it felt like we were in a Great Stagnation for a good while, why it sometimes still does, and why it feels other times like we're coming out of it. It's also important for us to understand how it is that we used to scrabble for alchemical ways to transform lead into gold just a couple centuries ago, and now land men on the moon.

A progress parable

To do this, and elucidate what standing on the shoulders of giants means, it helps to start with a parable that explains progress. That famous Connecticut Yankee who ended up in King Arthur's Court. After all, he also tried to use his modern knowledge to show strident and forbidden powers. His exploits, if you recall, included manufacturing gunpowder to use with guns, and using a lightning rod to blow up Merlin's tower. And much later in the book, when he gets captured, Lancelot rides to the rescue on bicycles he helped invent!

Which begs the question, or did to me anyway when I read it, why didn't bicycles and gunpowder exist in the 500s?

Gunpowder is a mix of Sulfur, Carbon and Saltpeter. Taoist alchemists in the early Han dynasty used to play with sulfur and saltpetre in their quest to find eternal life and alchemical transmutation, creating a flame that would "fly and dance violently".

But the first time it emerged from being a curious by-product of alchemy to a weapon was many centuries later. In the siege of Yuzhang, the troops shot a machine to let fire and burn the gate. The fire was from firebombs and arrows. Since early gunpowder needed oxygen for a proper flame, arrows in the air were as close to useful as they got. To become good enough for rockets you needed better gunpowder formulae. For that you needed better knowledge of chemistry and materials to build fire lances, and more. It took many more iterations before hand cannons became usable enough in combat where it had anything close to the functionality that the Connecticut Yankee needed.

Similarly, what does it take to make bicycles? Is having a spoke and wheel enough? A padded seat? An axle? Still no. If you want it to be in reasonably continuous operation, the trick is to overcome friction, which like most things to do with Newton is relentless. There needs to be ball bearings, something that would take a hell of a lot more innovation to create. Thinking "oh the bicycle is a simple machine" is to elide the entire world of complexity that's subsumed within each square inch of its frame. And that's without taking into account its materials of construction.

It turns out that even if our Yankee wanted to use both gunpowder and the bicycle, he would've had to rebuild a few centuries of knowledge to make it happen. Going back down the mountain of accumulated knowledge is a long road!

A pause in progress

So when we think about our history, that once upon a time our rate of wellbeing progressed very very slowly if at all, and then around the time of the industrial revolution it turbocharged, and then again recently we fell into another bit of stagnation, a cause could be that we found something extraordinary around the time of the industrial revolution, and figured out a way to use what we had far far better by the time of the revolution.

While there have been proponents of that philosophy aplenty, Robert Gordon on the pessimistic end and David Deutsch on the most optimistic end, the questions around why we're seemingly stuck in a productivity rut seem to have a few more proponents. Gordon for instance, thinks we've now used what we learnt all up, and have to be content with what we have or minor variations thereof with no more exponential growth.

Also both the points as to why we grew so fast before and why we're in a bit of a rut have the same answer - it's because of the way our growth and innovation actually comes about, by our ability to build new things atop what came before. Let’s have a look at a more topical example:

A specific historical example - vaccines

Vaccines have been one of those areas seeing multiple rounds of innovation, resulting in the invention that is supposedly going to change the face of medicine for a while. Let's have a quick run through some of the intermediate steps that we've taken to get here.

• 1796 - Edward Jenner found that cowpox protected against smallpox. The learning is that there are animal viruses can prevent similar human diseases, though there wasn't any sense of what viruses were at that point.

• 1868 - Friedrich Miescher discovered nucleic acids and RNA, since it was discovered in the nucleus

• 1885 - Louis Pasteur found that inoculations work. His thesis was that inactivated viruses could still train the immune system. This led to the influenza vaccine and the polio vaccine

• 1892 - viruses were discovered by Martinus Beijerinck by looking at filters from a diseased tobacco plant that infected other tobacco plants

• 1937 - Max Theiler attenuated yellow fever virus, introducing a series of genetic alterations, that helped humans carry it and induce immunity. The same technique then worked on polio, measles, mumps and several more.

• 1947 - Hypothesis on how RNA fits into gene function

• 1961 - mRNA was suggested by Jacques Monod and Francois Jacob, thinking in informational terms, and later discovered at Caltech

• 1980 - recombinant DNA technology helps create vaccines containing purified surface proteins from specific viruses, used in Hep B, papillomavirus and influenza.

• 2021 - SARS CoV-2 vaccine through mRNA, where the vaccines use mRNA, DNA or viral vectors that provide the instructions to cells on how to make the proteins. To get to the mRNA vaccines, we also needed insights into scaling up good manufacturing practices and instability of in vivo delivery.

At a simple glance, the pace initially was slow, with a roughly century long gap between the first few rungs. This substantially sped up in the middle of the 20th century, when innovations were coming every decade or two. And then, an almost forty year drought before the next big advance while a whole list of things that needed to be figured out got done.

Bear in mind this is still without taking into account the actual tools used. Whether it's the microscopes or computers in terms of hard technologies or scientific explorations and analytic methods in terms of softer social technologies, there have been hundreds of years of cumulative technological and scientific progress that went into making the above list come about.

If we take another look at the great work Katja Grace and team conducted looking at examples of discontinuous progress (i.e., the most highly consequential leaps) has done, it shows that same pattern of slow start, sudden explosion of creativity and progress, and then another stage of stasis.

We see a similar trajectory also in, say, physics. After an explosion in creativity and knowledge earlier in the century, the consensus seems that we’ve been hitting a rough path over the past few decades. What could explain this pattern?

As a solution, I suggest that innovation which leads progress is itself caused by combinatorial growth in its sub-domains, which first naturally creates accelerated growth, and later slowdowns as a result of a slowdown in any individual part or an increase in combinations to be tried. And once internalised, it explains all of the following:

• The exponential growth that we saw in the past couple centuries

• The genius clusters (e.g., Hungarian aliens) that seem to create and accompany it

• Why we will always have exponential input for linear output for individual technologies

• How a new innovation or technology emerges, and the actual shape of how a breakthrough technology cascades to the world

• Why occasionally will end up seeing periods of stagnation as the number of combinations to assess becomes too many

• And finally a way to break out of the great stagnation deadlock!

So onwards!

1. Progress comes primarily from technological innovation - the combinatorial S curves model

Unlike the technological pessimists who believe that our best days are long behind us, the technological worriers who think we ate all the low hanging fruit, and the technological optimists who think exponential growth is the base case and consequently just around the corner long as we get out of our own way, the answer seems closer to what Newton once said.

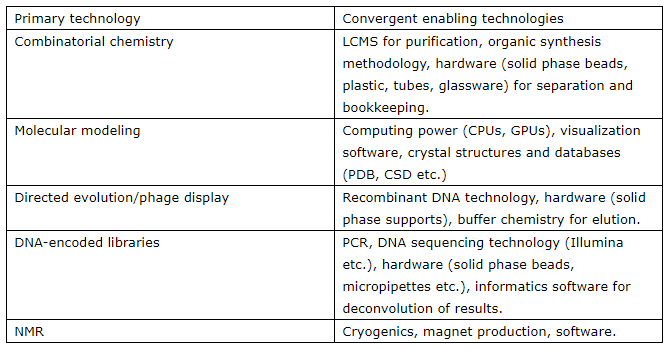
While we know about and opine about the fact of technological convergence, it's seen either as an obvious input or a curious outcrop within the progress narrative. Of course there's path dependence. For instance, Ash Jogalekar writes about how technological convergence helped Wright brothers make the first plane fly, because it relied on aluminium, aluminium molds, Hall-Heroult chemical process for refining bauxite and more. Similarly he derives the following chart of how this convergence helps, or could help, in drug discovery!

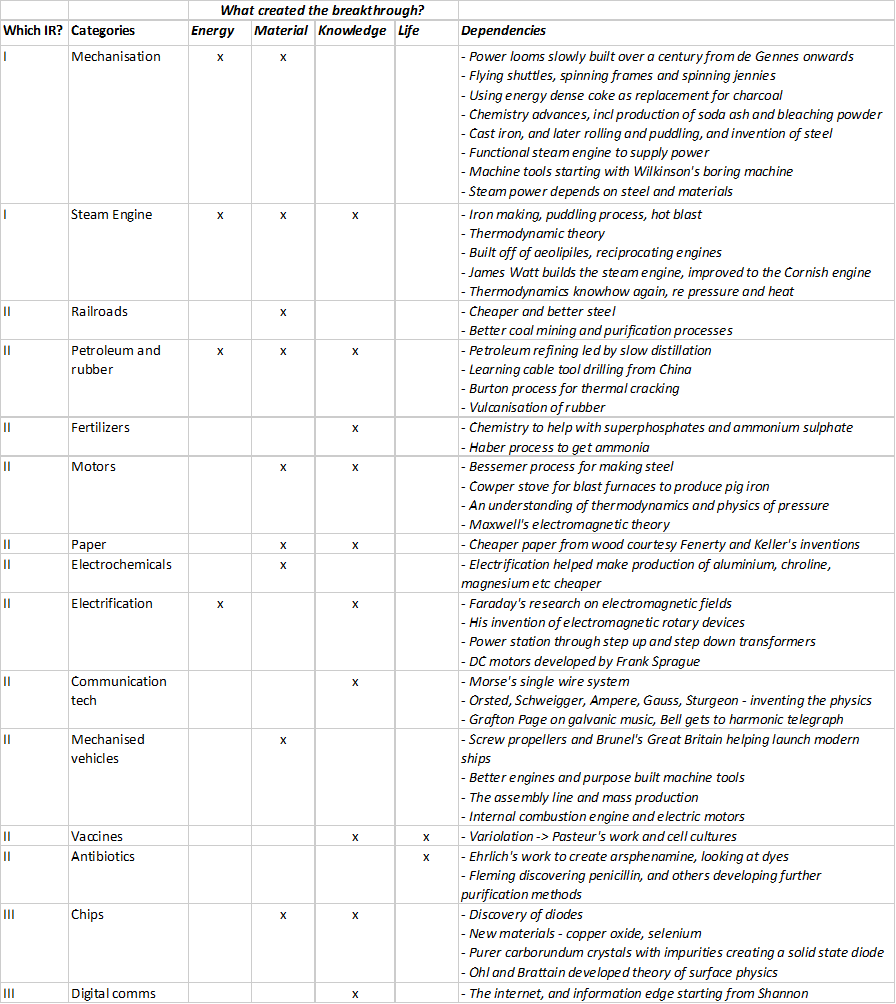
Similarly, to quote from my Isolated Narratives of Progress (which should've probably been called Narratives of Isolated Progress), we see that the major growth areas and categories that we've seen in the world have had multiple dependencies on minor and major advances across a whole bunch of technologies, which themselves had more, and so on and on. I map this against the four pillars of progress - energy, materials, knowledge and life, to utilise the first three.

The fact of the matter is that the general purpose technologies that we built, and which had disproportionate impact across all categories, they're few and far between. Once we built steel, it impacted everything. Once we invented electricity and the laws of electromagnetism, it affected everything. But getting to the benefits of both also required advances in chemistry, in manufacturing the right compounds, in thermodynamics, in automobiles and motors, and so much more, not to mention the advances in humanity-organisation-techniques that we were forced to invent along the way. They all reinforced each other in a positive feedback loop. Advances in one is what led to advances in the other.

So if we are to understand progress, we also need to understand how better to model these dependencies. Without an understanding of how we get to the next big innovation by continual combinatorial searches of the existing technologies we'll end up crafting narratives at the very macro scales (productivity increases with technology) or very micro scales (some innovators are especially good at finding the next GPT) without making enough progress in our understanding.

Most importantly, the growth we see shows an exponential curve. But exponential curves can be built without positing something special sitting in the crook of that L shape. They are the sum of growth trajectories that builds upon itself, treating progress as endogenous. Rather than posit a substantial cultural change, or mindset shift, or technological innovation, we use Occam's famous razor and see that progress could just have happened cumulatively.

Here I started by looking at the isolated narratives of progress and to try and forecast the next S curve. The key question was why there are speedbumps in the first place, and how they get created. And I modelled it as a combinatorial search over multiple S shaped innovation curves, like here - https://repl.it/@marquisdepolis/Innovation-test#main.r . This model of progress is built atop a few assumptions.

1. Individual technologies grow in an S curve diffusion pattern

2. New technologies emerge from the combinatorial interactions of existing technologies, as existing technologies act as complementary inputs to create a new technology, as long as the combination crosses a growing threshold

   1. Currently the level of complementarity is modelled as a product of all existing technologies - it's possible to replace it with a different function, even one that changes over time, as long as the essential characteristic that growth of new technologies in the future is dependent on knowledge already gained, i.e., it's a dependent and increasing function

   2. The threshold is also a slowly increasing function, for the same reason that the burden of new technology breaking above the growth rate increases with time, because you now need a much larger absolute impact to maintain the same percentage growth. Think impact of the wheel vs impact of an electric car. (You could also model this as a fixed threshold for emergence of new technology while the effort to do a combinatorial analysis of all existing technologies to come up with new ones also increases as the number of pre-existing technologies increase in number)

What's really important to understand about this idea of gradual progress is that if we believe in knowledge accumulation, and that science and technology grows by standing on the shoulders of giants, then progress is both endogenous and inevitable. It gives us a roadmap to follow, and tells us when we're likely to see periods of stagnation!

So what do we see as the output?

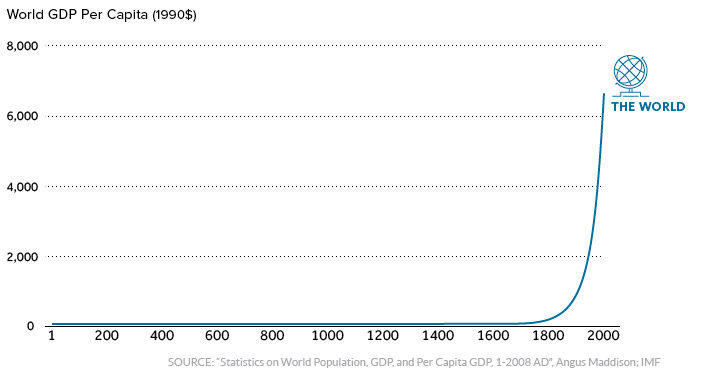
The GDP per capita curve stays relatively flat for the first 15 centuries or so. It's a global trend, this stands true in the Western world, but also in China, albeit with slightly different curvatures and starting points.

As we continue to explore what this model might look like it shows a few interesting aspects that explain our empirical evidence re roots of progress.

1. At first, the pace of technology development increases over time, as also the gap between individual new innovations decrease

2. The pace of innovations speed up around the year 1200 or so, and we start to see new clusters of innovations forming and growing

3. However as the number of innovations increase, the frontier to explore also increases, which then in turn creates longer gaps between innovations (note that this doesn't mean the impact of those existing innovations necessarily peter out during those gaps)

So the model looks pretty close to what we see in real life. Let's take a dive and see if the literature backs it up.

2. Breakthrough innovation comes from addition of novelty to existing paradigms, to drive the technological frontier

Does this hold up to historical scrutiny? Yes! First step is to have a look to see what the characteristics of this combinatorial view of innovation are and when it started to emerge.

(if you're not as interested in nerding out about academic papers feel free to skip to Part III below)

If you're curious when productivity growth began, in England it started in 1600s, well before the revolution. In a paper by Paul Bouscasse, Emi Nakamura and Jon Steinsson, they estimate this very thing:

We provide new estimates of the evolution of productivity in England from 1250 to 1870. Real wages over this period were heavily influenced by plague-induced swings in the population. ... In the early part of our sample, we find that productivity growth was zero. Productivity growth began in 1600—almost a century before the Glorious Revolution. Post-1600 productivity growth had two phases: an initial phase of modest growth of 4% per decade between 1600 and 1810, followed by a rapid acceleration at the time of the Industrial Revolution to 18% per decade. Our evidence helps distinguish between theories of why growth began. In particular, our findings support the idea that broad-based economic change preceded the bourgeois institutional reforms of 17th century England and may have contributed to causing them.

There has also been a fair bit of research into how innovation actually comes about as a result of recombining existing research areas. Research within a particular scientific discipline is thought to face some declining benefits, while getting insights from other disciplines is supposed to help increase the potential for it to become a breakthrough. A Matt Clancy article brought together some of the best papers in this domain (and parenthetically you should all subscribe to him).

A paper from Uzzi, Mukherjee, Stringer and Jones from 2013 discusses this in detail. Their conclusion is that innovation comes from a combination of novel ideas and the mainstream.

Our analysis of 17.9 million papers spanning all scientific fields suggests that science follows a nearly universal pattern: The highest-impact science is primarily grounded in exceptionally conventional combinations of prior work yet simultaneously features an intrusion of unusual combinations. Papers of this type were twice as likely to be highly cited works. ... Curiously, notable advances in science appear most closely linked not with efforts along one boundary or the other but with efforts that reach toward both frontiers.

The argument here is built on citations given and received vs what could've been expected based on an overall average. The resulting highest cited papers seem like they're highly conventional with just a little bit of crazy novelty in it. So if you're writing a highly conventional computer science paper and manage to sneak some Greek poetry into it, good work!

Similarly, Pichler, Lafond and Farmer's work show that innovation rate of a domain depends on the innovation rate of the technological domains it depends upon. i.e., if the domains you depend on for your work are innovating furiously, chances are you will too. This is of course closely related to the genius clusters that exists and seems to underpin most of innovation, and how cluster creation is the key aspect here. The insight is that technological domains do tend to co-evolve.

Similarly if we look at how we measure and assess innovation, we also see that they often seem the result of recombination of existing fields. A study of reclassification of patents, again by Lafond and Kim in 2019, shows how reclassification to a new sector (as a proxy for innovativeness of the paper and inability to classify cleanly) substantially increases citations (as a proxy for how great the paper is).

if classification changes reflect technological change, then one can in principle construct quantitative theories of that change.

Another paper, Garcia and Calantone 2002 also differentiates amongst innovations - Radical Innovations, Really new innovations and Incremental innovations. Radical innovations are the true breakthroughs, like steam engines of the world wide web, while the Really New are the macro breakthroughs like early telephone or electron microscopes.

In their analysis, Radical Innovation creates its own demand which was previously unrecognised by the customer (cue the bad quote about how there will be maybe 5 PCs in the world). To make this radically new, discontinuous S curve break out, the researchers need to investigate new approaches, draw up new lines of inquiry to be tested, and knowledge bases to be built, which requires exploration of the possibility frontier akin to discovering a new Kuhnian paradigm.

Put together, what's being shown here is that step-change innovations, whether that's what's seen practically within organisations, or in academia in terms of a highly regarded and cited paper, share the characteristics that they often push the boundaries of existing knowledge and try to recombine new pieces of knowledge, including some unorthodox permutations, to create the beginnings of a new S curve.

---

A Santa Fe paper called Logic of Invention by W Arthur in 2005 for instance talks about what's necessary to bring about truly original innovations, what they call the process of Origination. In a particularly evocative passage by mathematician Ken Ribet, talking about the process of coming up with a wholly new idea, he says:

The whole is a concatenation of sub-principles—conceptual ideas—architected together to achieve the overall purpose. Each component element, or theorem, derives from some earlier concatenation. Each, as with the sub-structures in a technology, provides some generic functionality used in the overall structure;

Similarly, the same process seems to play out within technology as well, as part of the combination/ accumulation view of progress.

A novel technology emerges from a cumulation of previous components and functionalities already in place. In fact, supporting any novel device or method is a pyramid of causality that leads to it: of other technologies that used the principle in question; of antecedent technologies that contributed to the solution; of supporting principles and components that made the new technology possible; of phenomena once novel that made these in turn possible; of instruments and techniques and manufacturing processes used in the new technology; of previous craft and understanding; of the grammars of the phenomena used and of the principles employed; of the matrix of specific institutions and universities and transfers of experience that lead to all these; of the interactions among people at all these levels described

And if we move away from the specifics of technological innovation and towards a more generic theory of how science is built atop previous science, it's worthwhile looking at the purer sciences. The best is of course mathematics, seeing as it's least dependent (at least until recently) on any externally available technology. And here it's interesting to look at this fascinating metamathematics analysis by Stephen Wolfram. If not perfectly analogous to our attempt here to map progress in terms of what has come before, it is at least directionally comparable.

He digs into Euclid's tomes and essentially maps them from initial axioms to full theorems. The map he draws is below:

Probably the most obvious thing is that the graphs start fairly sparse, then become much denser. And what this effectively means is that one starts off by proving certain “preliminaries”, and then after one’s done that, it unlocks a mass of other theorems. Or, put another way, if we were exploring this metamathematical space starting from the axioms, progress might seem slow at first. But after proving a bunch of preliminary theorems, we’d be able to dramatically speed up.

And equally importantly, he sliced this progress into time-periods, and tried to figure out how many "innovations", denoted by new theorems, develop in each subsequent time-period past the axioms. And what do we see?

Forget the colours for a minute, since they denote types of theorems, but the number of theorems that developed seem reasonably consistent after the initial set of axioms are proven. If this is any indication it's to demonstrate that there is some tradeoff between complexity of the axioms, since the later ones are demonstrably more complex, and the time it takes to unlock them.

So as time goes on, we get more and more complex theories, but not necessarily more theories. There's no a priori reason the same wouldn't be true of innovation. But if it were, we'd see spurts of growth and stagnation, and continuous growth, but at declining rates.

If you look at the lessons from all the papers cited above, they do tend to follow a similar pattern - subject matter comprising increasing levels of complexity are often identified by combining simpler pieces of understanding. And this is built up over time, as incremental innovations combine with radically new ideas to help create radical innovations which end up birthing entirely new segments!

3. This explains why our path of progress is exponential with occasional periods of stagnation

We set out to try and figure a cumulative, indeed compounding, nature of technological innovation, and how it's often build atop the wins that came before. This is a view that treats that growth and progress as endogenous, without requiring something substantially new, either in the form of culture or a technological breakthrough, to come about.

A combinatorial view of technological innovation, especially in line with its historically cumulative nature, helps us explicitly realise what's actually necessary if we want to push progress forward. For instance, it informs:

1. The observation that large general purpose technologies have had a hiatus, leading to a scientific and technological Great Stagnation; since technological convergence helps shape the way progress happens, as new innovations come together from multiple scientific and technological breakthroughs all coming together

2. Why certain technological developments develop in a "cluster", because if you want the product of previous technologies to show up above a threshold, then the previous technologies have to diffuse through, which happen as a cascade at particular times

3. The time between the clusters seem to increase over time as we wait for more of the combinations from amongst the technological frontier to get assessed, and to be seen as significant enough to impact the entire economy proportionally (i.e., creating a 1% growth impact in a $1 Trillion GDP vs 1% in a $1 Billion economy)

If the creation of a new technology requires a production function that's dependent on the number of previous technologies being analysed in some combination, naturally it'll increase in effort as the number of previous technologies increase - there's just more combinations to explore. Similarly if the pace of development is dependent on the ability to test all the possibilities at the frontier, or at least test enough of them that you find a winner, that would indicate that technology breakthroughs on which progress depends requires much more of this kind of exploration.

So if Complexity of analysing and combining existing technologies > Innovation Threshold, then there's potential for a new innovation to start up and break through, much like Wright brother's plane or SpaceX figuring out a way to launch cheaper, reusable, rockets.

And when this happens, there are a couple of consequences.

Ceteris paribus, the gap between subsequent technological innovations will get longer as time goes on. This is because the "effort" function increases as time goes on. In the current formulation, the increase is driven by the number of possible combinations of previously existing technologies that you have to explore before hitting a "winner". And that only keeps increasing as we explore further. The continuation of our exploration expands the frontier, increasing the search area.

Another key insight is that the "next big step" is dependent on not only our ability to synthesise knowledge and identify promising new tangents to explore, but also on the sheer difficulty of doing so. In the model this is the interplay between the effort function and the threshold function.

What's highly interesting is that we have been able to somehow keep pace thus far. One of the main reasons is that the increasing population and the fact that we have been able to keep "time to insight" low means that we have been able to buck this trend. Why does increasing population matter? Because it brings an exponential trend also to the researchers entering and exploring any field, which masks the increasing difficulty of idea-space exploration.

4. The implications and conclusions

Summary

1. Progress seems to come primarily from innovation and technology

2. A Kuhnian paradigm shift or the emergence of a new breakthrough innovation is a result of a combinatorial exploration of existing technologies

   1. Technological innovation in any one field shows up in the form of an S curve

   2. Several S curves add together to create exponential growth

   3. To break through requires the innovation to be above a certain threshold, which itself increases over time as we make more and more discoveries

3. Breakthrough innovation comes from the addition of novelty to existing paradigms - this requires a "search" of the actual technological frontier, which keeps expanding

4. Depending on the level of progress of each S curve, occasionally you'll have periods of stagnation while the search for right combinations is ongoing

   1. If the number of existing fields is too large, the search can take longer, while we wait for the right combinations and the right level of progress amongst the component technologies

   2. Bridging that gap requires sufficient progress in more individual technologies, and more collaboration amongst technologies

   3. This might feel like a stagnation, but that's only because without the emergence of new paradigms or new breakthrough innovations, we're at the far end of an S curve, where you need exponential inputs for linear outputs

The optimistic case for progress has a clear narrative too. Humanity has, so far, always figured out a new technological frontier to continue our progress. (However as financial advisors all say, past performance isn't indicative of future performance.) And while there is a theoretical limit to growth, unless you write off Dyson spheres as implausible, we have a ways to go before we hit them.

They can create a narrative whereby we are the architects of our own stagnation, through our stubborn refusal to work towards progress. But this misses the fact that while we have indeed, so far, figured out several new technological frontiers, they don't appear de novo.

The pessimistic case is best made however by Bloom et al. That argument was delved into some depth by Scott Alexander who finished his piece by asserting that "constant progress in science in response to exponential increases in inputs ought to be our null hypothesis". That conclusion effectively is underlined by the fact that while we've had huge increases in the number of researchers, the actual research output hasn't changed much. We can see this of course in semiconductors but also in theoretical physics!

It also indicates that this is clearly an unsustainable trend - it will end with a larger and larger fraction of the population becoming researchers, and eventually us running out of people! (I explored this also in some depth in the "Technological stagnation" section of The Great Polarisation.)

Productivity of a process, whether that's startups trying to expand or scientists inventing the next big thing, are subject to the law of diminishing returns. They will find that initial traction is easy while subsequent traction gets harder and harder.

There's a big difference between "work exponentially hard to squeezes the stone and find new ideas" vs "work exponentially hard to find a whole new paradigm". The first is what necessitates exponential increase in researchers to discover the next piece of insight from within a paradigm.

But as Kuhn would point out, the emergence of a new paradigm opens up new vistas. Unfortunately we can't tell how or when it might open up. Maybe banging away at the seams of the existing paradigm is what's needed. Maybe it's trying to find new paradigms directly. Maybe it's throwing smart people from multiple disciplines together and hoping for the best.

Regardless, that path of breaking through a paradigm isn't guaranteed, nor is it predictable with any degree of accuracy. We can't tell whether a pause in productivity growth of a few decades is cause for concern or just a blip or a random adjustment period.

My conclusion here is that the dips we see are because the level of specialisation we have achieved increases the level of coordination that's required to get the benefits of one field to another. You could call us victims of our success, though that would be too pessimistic.

Knowledge is naturally accretive, though knowledge also requires chiselling out of raw marble to generate. If we need to continue our paths what's concretely needed is tools and norms and institutions to help explore the idea-frontier better.

We don't need to jump off a cliff in sadness at the thought that our physicists aren't as productive as those in the mid-century. And we shouldn't jump off a cliff in joy that mRNA vaccines show us the path to a brave new world.

This would be the time for some intellectual humility.

This matters precisely because this is not the general narrative which swings between wild optimism that the Stagnation has ended (space, global vaccines, quantum computing) or that we're all one step away from doom (inequality, productivity chasms, Moore's law ending). We still shuttle between arguments on population growth dynamics or Blooms argument being taken too literally that it's equivalent to Fukuyamas end of history. Or even worse, the assumption that the slowing of growth for a while comes from some ahistorical unique confluence of events that we must slay like an itinerant dragon.

Questions like this is why I like Progress Studies as an idea and a concept. I wrote a proposal for how we might be able to go about it here. I think interdisciplinary research is woefully underrated and underexplored. And I think asking some of these questions is extremely important. To quote:

In fact the rise of interdisciplinary studies in universities seems to point at this very issue that everyone seems happily ensconced in their own ivory tower without being able to make bridges to each other's. And while that sounds like an easily solved issue, turns out to actually transfer real knowledge is much harder. After all nobody who actually lives in an ivory tower likes to schlep all in the way down, find a decent crossing, then work their way back upwards another tower.

But we should be not be looking at every dip in a graph as evidence of a Stagnation, or call it the outcome of some failed policy. Quite often we don't know if it's just part of the natural variation. It's important to admit that. And it's also important to admit that the current data can be explained by a dizzying array of hypotheses, so perhaps a bit of patience is warranted.

5. Some suggested next steps to explore

There are several areas of course which would need to be further explored to flesh this out as a theory better, both qualitative and quantitative.

1. There's randomness in the world that impacts all aspects of both technology development, and makes the curves seen here much less smooth - for instance WWII helped push manufacturing technology along quite a bit!

2. There is also an analysis needed here of the actual clusters of geniuses who set matters in motion to identify and expand on radical technological innovations

3. A trial to explicitly define specific growth paradigms according to - e.g.,

   1. GDP growing primarily due to population, e.g., a Malthusian model

   2. Growth coming from per capita income rise via technology

   3. Growth explicitly coming from increased population dynamics

4. There is no analysis here of technology obsolescence, where older, pre-existing, technologies have a slow demise. This is implicitly taken care of in the model where older technologies reach maturity and then stay in stasis, but needs to be spelt out also to figure out both senescence of old tech and recombination to create new fields.

5. Different General Purpose Technologies might play differing roles in potential growth as they have different diffusion patterns, and different eventual amplitude, how can we model that?

6. An analysis of how inclusion of more optional combinations would change the form of growth - whereby there are multiple paths to similar growth trajectories and we just need to choose one, how does that change the path?

7. How will change in our lifespans/ health affect this growth trajectory?

8. How does changing leisure time or education help increase this trajectory - for instance by giving people more time to dabble in more fields and thereby increasing the combinatorial exposition time?

The benefit we’d have in trying to understand how innovation and progress comes about is immense. For prosaic reasons like scientific funding allotment and more philosophical considerations, its a mystery worth solving!

Appendix: A few other explanations

Foundational vs incremental innovation

It's difficult to say which is which except after the fact. This is also a form of "low hanging fruits have been eaten" argument. It's incredibly early, but the current efforts in material science, quantum computing, mRNA vaccines and more belie the fact that there aren't entirely new fields of study emerging.

We're highly innovative but the world is too big

The theory is that it just doesn't show up in statistics because the overall size of the pie is so much larger. But this doesn't make sense unless the inventors today, who are much more numerous, are all working independently with their efforts not impacting each other. So while this helps explain why we don't have individual inventors who are of the same stature as Lord Hargreaves, it doesn't help explain why the societal impact of innovation is still limited.

Innovation is a contagious disease

Dr. Anton Howes explores innovation as a contagious disease and lays out an elegant hypothesis that innovation spreads because of a particular mindset, which only became prevalent, through accident or otherwise, in pre-Industrial revolution Britain.

I have a lot of sympathy for this line of argument. For one thing I've written about the role of "genius clusters" in most step-change innovations that we've seen, and there seems to be an outsized role that these clusters play in our overall progress.

Where I disagree is that the cluster formation being the necessary spark, rather than the underlying technological change being the necessary spark to create those clusters in the first place. There were clusters of like-minded, curious, smart intellectuals who got together in every civilisation at every point in time across world history. Yet it remains true that few of them got to escape velocity. It can't be that the contagion of a particular (and rather straightforward, though with hindsight bias) form of thought on "improvement mentality" is what would give rise to it.

For one example, looking at any ancient architectural miracle is a fractal like effort of finding newer and even more amazing innovations the deeper you go. First the overall complex, then the walls, then the buildings, then the carvings on those buildings, then the structural points amongst those carvings. And so on and on. Each artisan, unnamed though she may be, worked tirelessly to improve their craft.

Exponential growth can be our baseline

Were we to focus on the fact that historically we've seen exponential curves come and sustain themselves, we often see this is because of the emergence of new innovations in a timely fashion rather than an intrinsic ability for technology to compound. For example, Jason Crawford from the Roots of Progress starts his piece asserting:

My first reason for an exponential baseline is that we have plenty of historical examples of exponential growth sustained over long periods. One of the most famous is Moore’s Law, the exponential growth in the number of transistors fitting in an integrated circuit

But Moore's Law is also famous exactly for breaking the exponential trend once it hit the physical boundaries that it cannot cross. It, more than anything else, exemplifies the fact that we cannot have exponential growth forever and that all paradigms have their natural end point.

Population growth

As humans we first hacked this by increasing our population size. This solved the problem nicely for a while. But then we got richer as a species and our population growth rates plummeted.

Frustratingly this does explain a fair bit of the seeming stagnation and growth beforehand, assuming ideas per population is roughly constant. This would be an area that merits further investigation!

Coda

So are ideas getting harder to find, like Bloom mentioned? Yes they are. Within any individual paradigm ideas always get harder to find as it matures. But that's not the story.

The story is that we have moved from a world where ideas are getting harder to find, but we discover new sources of ideas anyway, to a world where ideas are getting harder to find and we discover new seams to mine for ideas more sporadically.

Occasionally the progress might cluster when a general purpose technology reaches critical mass, but that is not predictable either.

• Either you wait until a new GPT reaches maturity, when the steep drop in per unit cost makes it applicable to every other sector

• Or you wait until the combinations of existing technologies can be applied to new sectors, which gets more complex as the number of combinations to try increases