Binary outcomes in multidimensional space
Sometimes iterated games don't look like iterated games and we make decisions that feel like one-time outcome maximisation
I
Say you're working for Acme Inc. They make widgets of an unspecified but awesome nature, manufacture them in China, ship them to the US, get people to buy them, and make bucketloads of profit. So far, so generic. Your job is to help tell the CEO and the Board what they should do the next year so they can make even more bucketloads of money.
Tell them to do what they're doing so far, just better
Tell them to do something new, like Bacme Inc does, by selling things online/ having an app/ creating sexy ad campaigns and attracting younger people etc etc.
No matter what idea and justification you come up with, there's an issue. The company can only do one thing. And if you think there are 5 possible actions, and say 10 possible ways of completing that action successfully, suddenly you have at least 50 ways of doing things. How do you tell Acme not only which 1 out of 5 ideas they should do, but also which 1 out of 50 paths they should take?
And even more importantly, how do you know if you made the right call next year? If everything comes up roses, is that because you were a supersmart genius, or because you lucked out? If everything goes to hell is that because you're a moron or because sometimes that's just what happens?
Playing with multidimensional objects is hard, and dimensional reduction always results in information loss. This means that there's always going to be situations where the amount of information that is actually used to make a decision is lesser than the total amount of information that actually exists.
There's an argument in management theory about the benefits of having extraordinary CEOs. In fact this was one of the key tenets of the modern organisational world, where CEOs get paid 300x more than the average employee.
In some ways it's difficult to argue. If you lead an organisation worth $10B, and one of your ideas makes it be worth 1% more, that's $100M that you've just made. Who could begrudge you taking a bite out of that?
On the other hand, if you were going to make $10.1B anyway, with the average CEO efforts being no better than random darts thrown by a friendly chimp, then you're just spending useless money giving a portion of that to the CEO.
Actually it's even worse than that. You're spending money to incentivise someone to take unnecessary and crazy risks. If they're wrong, they still get paid big bucks. But if they're right they attain the musky aroma of corporate Godhood.
That's the curse of the binary outcome. It hides the entire painful process.
There's a similar problem in politics. Victories are binary, but the margins are tiny. You win an election in one corner of the country by a few hundred votes, you win the whole damn thing. Just like in business, a small advantage is the difference between winning a hand and losing a hand. There really are only two outcomes possible. In other words, we live in a binary world.
A large part of our daily life falls into the same pattern - binary rewards on uncertain odds. In poker, all good players will tell you, the benefit is that the odds eventually stack up. If you always have a 51:49 advantage, then if you play enough hands, those odds give you an extra couple hands every 100. It's only the repeated playing that eventually evens out the score. It's only when you add up multiple binary events that you can reach an eventual "success" state.
But even though it makes statistical sense, for most players it doesn't make intuitive sense. They think in terms of "I almost had it" or "that last card tripped me up" or "my opponent got lucky with that King of Clubs". All true, but irrelevant.
It's the difference between winning battles vs winning a war. Everyone focuses on the battle, very few on the war. Jeff Bezos, whose Amazon empire will soon swallow all that it sees, said that planning on a longer time horizon is an essential ingredient to success, because so few people do it. Again, focusing on the war, not the battle.
Thinking probabilistically is great and all, but life is often binary. Why does it seem that way?
II
Sometimes it's difficult to play poker against complete beginners. They do dumb things like calling all the way to the end with a 7-7 pair, and often (but not too often!) can get lucky with another 7 on the River. In fact it should happen 4.2%, or rather once every 25 plays.
Luck is a weird concept. Two of the key ideas around luck thinks that it's is either (1) an artefact of our lack of knowledge about a system. Or (2) It's an artefact of the randomness inherent in the world, where it's not just our knowledge of events but rather the uncertainty inherent in the world. It's as true of luck, as of probability itself.
Within our poker plays, it's often the former that comes to play. For example if you had known that the River was a 7, then there is no luck involved anymore. Neither is there any uncertainty.
When conflating luck with talent or foresight becomes easy, it gets harder to create any sort of process to dig deeper and win.
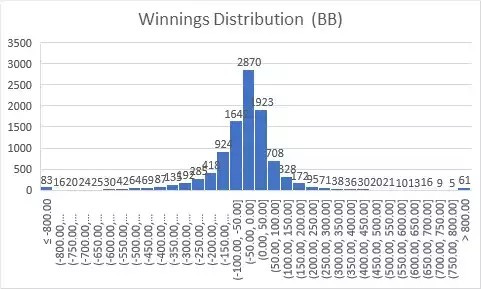
So when you're playing, chances are that your outcomes and up converging. If you're a fish it'll end up pushing you to the extreme of zero. And if you're good it'll push you towards the other extreme. The distribution of outcomes is quite instructive.
Those in the middle of that distribution will have middling outcomes, but they're not going to substantially affect the monetary outcome in a game. There'll be a normal distribution that emerges.
If you add in all those who just paid in once and lost it all, the distribution changes, and adds another normal distribution with a tiny mean and mostly skewed towards people losing their whole buy in.
In any single hand this would be a highly skewed outcome. As they probabilities accrue, the whole game statistics becomes a bit more straightforward to compare, in line with the probabilities.
But there are also two key demographics to compare atop. Ones the professional kind, with high skill and ability. And another's the regular casual gamblers who just want to have fun and try. The middle ground of those who play a lot but aren't great isn't a large component. This means that on a long enough timeline the distribution begins to look like a power law curve.
III
This phenomenon also recurs in other areas too. We all want to engage in games where we have a clear ability to win, which means a game with a high probability of us being at the top of the field. Then there are those games where we're newbies and play for fun.
In politics there's the occasional candidate from left field, but there majority have clear outcomes. It's the politicians that win political elections. It's the epitome of a non-recurring binary event, so we shouldn't be surprised at the outcome. You don't play the game unless it's your livelihood, or there's a clear plan B for when you lose.
Let's look at the rational world of investment banking. Bankers do exactly the same in helping buy companies or doing high visibility deals and projects. They get far more benefits outside of the actual outcome of the decision.
How about science? Scientists of course want to focus on the high potential research areas, so that's where they cluster. But if there's a fair amount known about what's fashionable and likely to pan out, it's also possible that only the A+ students get to work on it and make that incremental progress! The B+ students however work on things they find exciting and occasionally discover DNA. (The C+ students of course leave academic pursuits and make the real money).
Some of it is about the ubiquity of binary games in life, and the strategy that we ought to take to play them. If you're at the top of the distribution you're fine to play - you're whom the game was designed for. For the others there's a gamble to be made.
There problem arises when these binary distributions make us update our priors about knowledge too strongly compared with a probabilistic outcome. That's sort of the whole point. It exchanges high levels of clarity for epistemic fog.
When the distributions aren't repeated often, this fog gets thicker and thicker.
In life we come across areas where we have to make decisions on ideas and items all too often. Most of business, and politics, and economics, and healthcare, and life, is like that. There aren't any obvious repeated games. We don't feel like we're in the middle of a repeated prisoner's dilemma even when we are.
Trying to optimise a single decision is akin to playing with unknown probabilities. If there aren't enough ways to be proven wrong regularly our beliefs can't help but ossify in convenient fashions.
If a binary outcome changes your belief in terms of future potential, you tend to think more in terms of probabilistic beliefs. Therefore, if anything process matters even more.
So if you're making decisions in areas where the outcomes are binary, and you don't think it'll recur often enough, it's worth keeping in mind that Bayes might trip up!